Mixture and Allegation
Mixture and Allegation
Concepts
Essential Blocks Advance Subtitle
Mixture and Alligation Concepts for GRE
Mixture and alligation problems appear frequently in GRE Quantitative Reasoning, challenging candidates to solve for unknown quantities in mixtures with different properties. This guide provides the fundamental concepts, formulas, examples, and practice questions to help you master these types of problems.
1. Mixture Problems
In mixture problems, two or more substances with varying concentrations, prices, or other characteristics are combined. The goal is to find the resulting mixture’s concentration or the required amounts of each component to achieve a desired result.
Key Formula for Mixture Problems
When two substances with different concentrations are mixed, the resultant concentration ![]() is calculated as:
is calculated as:
![]()
where:
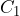 and
and  are the concentrations of the two components.
are the concentrations of the two components.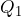 and
and 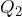 are the quantities of each component.
are the quantities of each component.
Example 1: Mixture Problem
Problem: A chemist has a 20% saline solution and a 50% saline solution. How much of each solution must be mixed to obtain 10 liters of a 30% saline solution?
Solution:
- Let
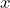 be the quantity (in liters) of the 20% solution, and
be the quantity (in liters) of the 20% solution, and  be the quantity of the 50% solution.
be the quantity of the 50% solution. - Using the formula for resultant concentration:
![Rendered by QuickLaTeX.com \[ 0.20x + 0.50(10 - x) = 0.30 \times 10 \]](https://gre.mksprep.com/wp-content/ql-cache/quicklatex.com-bf273798d6685cf90bcd74d1f2cadb42_l3.png)
- Simplify:
![Rendered by QuickLaTeX.com \[ 0.20x + 5 - 0.50x = 3 \]](https://gre.mksprep.com/wp-content/ql-cache/quicklatex.com-555edd75ccb9601d9050fb6a769e1d1e_l3.png)
![Rendered by QuickLaTeX.com \[ -0.30x = -2 \]](https://gre.mksprep.com/wp-content/ql-cache/quicklatex.com-5722db09e2887f94d8af23ef23a0330d_l3.png)
![Rendered by QuickLaTeX.com \[ x = \frac{2}{0.3} = 6.67 \]](https://gre.mksprep.com/wp-content/ql-cache/quicklatex.com-989689517affcb6649566c0835c40ef2_l3.png)
- Therefore,
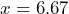 liters of the 20% solution and
liters of the 20% solution and 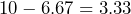 liters of the 50% solution are needed.
liters of the 50% solution are needed.
2. Alligation Method
The alligation method is a simplified approach to solving mixture problems, particularly useful when two ingredients with known concentrations or prices are mixed to reach a target concentration or price.
Alligation Rule
The formula for the alligation rule is as follows:
![]()
where:
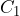 and
and  are the concentrations or prices of the two components.
are the concentrations or prices of the two components.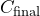 is the target concentration or price.
is the target concentration or price.
3. Additional Examples
Example 3: Mixture Problem
Problem: A milkman has milk with 10% fat content and another with 30% fat content. How much of each type should be mixed to create 50 liters of milk with 20% fat content?
Solution:
- Let
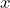 be the quantity of 10% fat milk, and
be the quantity of 10% fat milk, and  be the quantity of 30% fat milk.
be the quantity of 30% fat milk. - Using the concentration formula:
![Rendered by QuickLaTeX.com \[ 0.10x + 0.30(50 - x) = 0.20 \times 50 \]](https://gre.mksprep.com/wp-content/ql-cache/quicklatex.com-dcf2a560f8737ffa13ecb3b4dafc4644_l3.png)
- Expanding and solving:
![Rendered by QuickLaTeX.com \[ 0.10x + 15 - 0.30x = 10 \]](https://gre.mksprep.com/wp-content/ql-cache/quicklatex.com-10261eb4101cfefde9abf8432ae5f951_l3.png)
![Rendered by QuickLaTeX.com \[ -0.20x = -5 \]](https://gre.mksprep.com/wp-content/ql-cache/quicklatex.com-54ea8c6706704d03a8f385d375a242ce_l3.png)
![Rendered by QuickLaTeX.com \[ x = 25 \]](https://gre.mksprep.com/wp-content/ql-cache/quicklatex.com-c0d5a1f1d143605b35e63766fc1dc2a3_l3.png)
- Thus, mix 25 liters of 10% fat milk with 25 liters of 30% fat milk.
Example 4: Alligation Problem
Problem: A perfumer has essential oils priced at ![]() 15 per ounce. He wants to create a blend priced at $12 per ounce. In what ratio should he mix these oils?
15 per ounce. He wants to create a blend priced at $12 per ounce. In what ratio should he mix these oils?
Solution:
- Set up the ratio:
![Rendered by QuickLaTeX.com \[ \text{Ratio of Quantities} = \frac{|15 - 12|}{|8 - 12|} = \frac{3}{4} \]](https://gre.mksprep.com/wp-content/ql-cache/quicklatex.com-8e08f58963be58ccc1d9b3f4df930fc4_l3.png)
- Therefore, he should mix the oils in a
 ratio to achieve the desired price.
ratio to achieve the desired price.
4. Practice Questions
Practice Question 1:
A solution contains 30% alcohol. How many liters of pure alcohol should be added to 20 liters of this solution to make it a 40% alcohol solution?
Practice Question 2:
A jeweler has two gold alloys: one is 30% pure gold, and the other is 70% pure gold. In what ratio should they be mixed to get an alloy that is 50% pure gold?
Practice Question 3:
A beverage company has two fruit juice concentrates, one with 25% fruit and the other with 55% fruit. How many liters of each should be mixed to make 60 liters of a concentrate that is 40% fruit?
Conclusion
Mastering mixture and alligation techniques enables you to efficiently tackle GRE questions on combined solutions or costs. Practice with various scenarios to strengthen your skills and improve your problem-solving speed.
Time-bound Tests
These timebound tests are similar to real Tests
Test – 1
